Double hashing

Double hashing is a computer programming technique used in hash tables to resolve hash collisions, cases when two different values to be searched for produce the same hash key. It is a popular collision-resolution technique in open-addressed hash tables.

Like linear probing, it uses one hash value as a starting point and then repeatedly steps forward an interval until the desired value is located, an empty location is reached, or the entire table has been searched; but this interval is decided using a second, independent hash function (hence the name double hashing). Unlike linear probing and quadratic probing, the interval depends on the data, so that even values mapping to the same location have different bucket sequences; this minimizes repeated collisions and the effects of clustering. 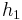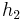In other words, given independent hash functions h_1 and h_2, the jth location in the bucket sequence for value k in a hash table of size m is:

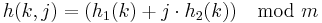
h(k,j)=(h_1(k) %2B j \cdot h_2(k))\mod m

Disadvantages

Linear probing and, to a lesser extent, quadratic probing are able to take advantage of the data cache by accessing locations that are close together. Double hashing has larger intervals and is not able to achieve this advantage.

Like all other forms of open addressing, double hashing becomes linear as the hash table approaches maximum capacity. The only solution to this is to rehash to a larger size.

On top of that, it is possible for the secondary hash function to evaluate to zero. For example, if we choose k=5 with the following function:

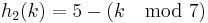
h_2(k) = 5 - (k\mod 7)

The resulting sequence will always remain at the initial hash value. One possible solution is to change the secondary hash function to:

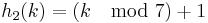
h_2(k) = (k\mod 7) %2B 1

This ensures that the secondary hash function will always be non zero.

Basically Double Hashing is hashing on already hashed key.

See also

External links